Tree
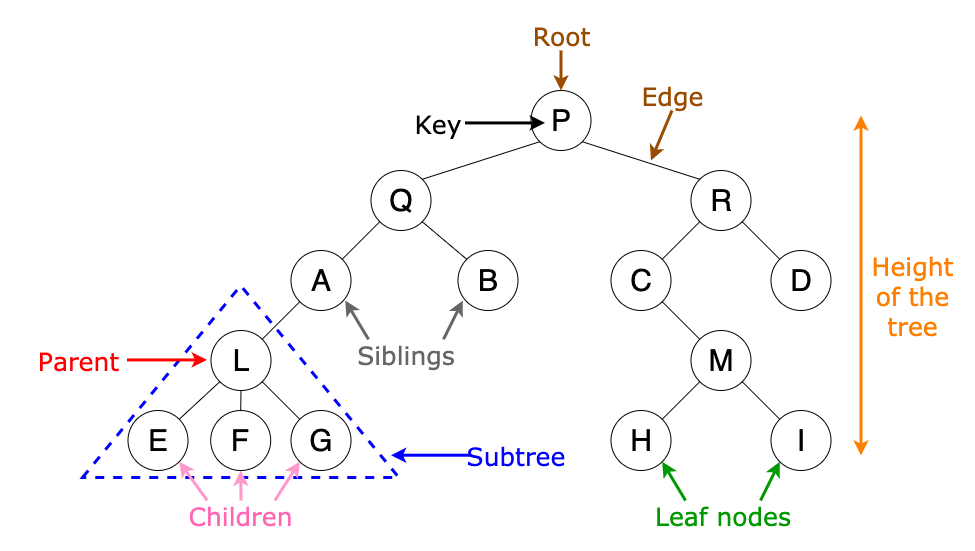
What is meant by tree in data structure?
- A tree is a non-linear data structure represented in a hierarchical manner.
- It contains a finite set of elements called ‘nodes’
- These are connected to each other using a finite set of directed lines called ‘branches’.
- Children of same parent are called Sibling.
- Top most element of node is called the root node.
- The node which do not have any child is called leaf node.
- The node that has atleast one children is called internal node.
- Trees can also called as recursive data structure.
Various Tree terminologies
Parent:The parent of a node is the immediate predecessor of that node.
Child:The immediate successor of a node are called child nodes. A child nodes which is placed at left side is called left child. A child which is placed at right side is called right side of a node.
Siblings:The child nodes having the same parent is called siblings.
Root:A root is a special designated node in a tree structure. It is a node which has no parent . There can be only one root node in any tree structure.
Leaf nodes(External nodes) :A leaf node which does not have any child nodes.
Internal nodes:Internal nodes which is having a parent and atleast one children are called internal nodes.
Branch and Edge:It is connecting line between two nodes . A node can have more than one edge.
Path:Each node has to be reachable from root to a unique sequence of edges is called a path. The number of edges in a path is called length of the path.
Degree of a node:The number of edges connecting of a particular node is called the degree of a node.
Degree of a tree:The maximum number of a degree of a node is called the degree of a tree.
Level of a node:The level of a node is the number of edges along the unique path between it and the root level of the root is defined as ‘zero’.If a node is at level I, then it childrens is at level I+1.This rule is common for all the nodes except the root node.
Height and depth of a tree: The maximum number of a level of a tree is called its height and depth of a tree. In other words, we can say the height of a Tree is the height of the root node or the depth of the deepest node.
Height of a Node: The height of a node is the number of edges from the node to the deepest leaf (ie. the longest path from the node to a leaf node).
Depth of a Node: The depth of a node is the number of edges from the root to the node.

Binary tree
- In binary tree, each node can have atmost two childrens.
- A binary tree, it is either empty or it consists of a node called ‘root node’, it having two childrens, called left subtree and the right subtree of the root
Or
A binary tree , it is either empty or it consists of almost two childrens of a node.
Basic structures of Binary Tree
- In this tree, codes either have 0 or 2 children.
- We could have a node with just one child as left child or right child.
- A node with zero childs is called leaf node.
Properties of a Binary Tree:
- A binary tree has n number of nodes, then the number of edges are n-1.
- For a non-empty binary tree ‘n’ is the number of nodes and ‘e’ is number of edges.
n=e+1
The total number of nodes in a binary tree is atleast 2n +1 and atmost 2n+1+1.
- The minimum number of nodes in a binary tree of height h is ‘h’.
- The number of internal nodes is atleast h and atmost 2h-1.
- The height of a binary tree with n nodes atleast (logn+1) and atmost n.
Types of a Binary tree
We have so many binary trees such as:
- Complete binary tree
- Almost complete binary tree
- Strictly binary tree
- Left skewed binary tree
- Right skewed binary tree
Complete Binary tree
It is a binary tree in which all leaves are at same depth . The total number of nodes at each level has 2i.
- The total number of nodes in a complete binary tree has 2h+1-1,
where h is the height of the tree.
Almost complete binary tree
- It is a binary tree which has two rules:
- Each node has left child, wherever it has a right child that means it is always left child but for a left child there may not be a right child.
- The leaf in a tree must be present at height of h or h-1.
Strictly Binary tree
A binary tree is a strictly binary tree if and only if each node has exactly two child nodes or no nodes.
Left skewed binary tree
A binary tree is a left skewed binary tree if and only if which is each node having its left child only.
Right skewed Binary tree
A binary tree is a right skewed binary tree if and only if which has each node having its right child only.
Binary tree can be represented in any way of the following two ways:
- Using an array(Linear representation)
- Using a linked list(Linked representation)
- Using an array(Linear representation)
A binary tree can be stored represented by using arrays, which is called sequential or linear represntation. This type of represent is static means that a block of memory for an array is to be accurated before going to store the actual data.
- In this representation, the nodes of the tree are stored level by level starting from the root node . The root node of the tree is stored in the first memory location of allocated memory.
- The following rules are used to decide the location of any node in the tree structure:
- The root node is at location 1.
For any node with index i, 1≤i≤n
a) Parent of (i) =i/2
b) Left child (i) =2i
c) Right child(i) =2i+1
Advantages
- The data are stored without any pointers.
- Any node can be accessed by calculating the indexes.
- Simplicity
- Static memory allocation.
Disadvantages
Array representation is not suitable for normal binary tree, but it is only ideal for complete binary tree.
- Here most of the array a trees are empty means that more memory is wasted unnecessarily.
- Additions and delicious of nodes are inefficient because of the data moments in the array.
- To overcome all these problems by using linked list representation.
Using a linked list representation
- The binary tree can be represented by using dynamic memory allocation of a node in the linked list form. It contains three fields.
a) Info(data) :It contains the actual data of a node.
b) Left link(left) :It contains the address of the left sub- tree.
c) Right link(right) :It contains the address of the right sub-tree.
When a node has no childrens, the corresponding pointers fields(left, right) are “NULL”.
Advantages
- No wastage of memory.
- Insertions and deletions involves no data moment.
- Dynamic memory allocations.
Disadvantages:
- In this the pointer fields occupy more space than data field.
- Programming languages which do not support dynamic memory allocation have difficulty in implementing binary tree.